How to Identify & Remove Empty Columns in SAS

As a SAS Programmer, you sometimes need to import data from an external source, for example, an Excel file. After importing your Excel file, you might discover that your imported data contains empty columns. In this article, we demonstrate how to identify and remove empty columns in SAS.

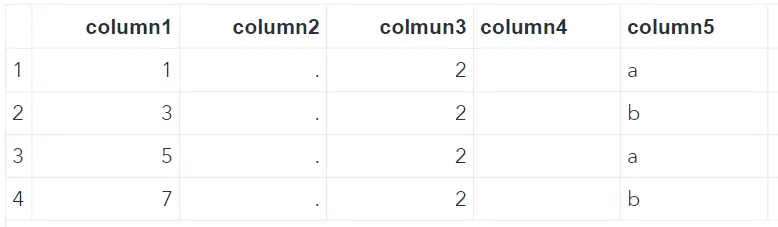
For the examples in this article, we create a SAS dataset with 5 columns of which 2 are empty (column2 and column4). We do this with the datalines statement and the missover option.

/* CREATE A DATASET */
data work.my_data;
	infile datalines dlm="," missover;
	input column1 column2 colmun3 column4 $ column5 $;
	datalines;
1, ,2, ,a
3, ,2, ,b
5, ,2, ,a
7, ,2, ,b
;
run;

How to Identify Empty Columns in SAS

First, we need to identify the empty columns before we can remove them. We could do this by visual inspection and remove the empty columns with a drop statement. However, if we want to create reusable SAS code, this isn’t the best option. The structure of your imported data could change and/or the imported doesn’t always contain empty columns.

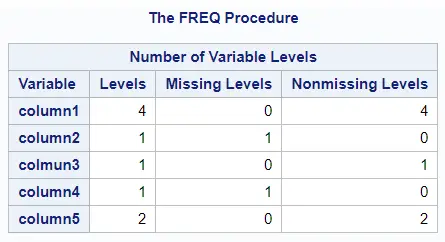
With the FREQ procedure, you can identify the empty columns in your data with SAS code instead of by visual inspection. One of the PROC FREQ options is the nlevels option. This option shows you:

• The Levels per column, i.e. the number of distinct values. A missing value is considered as a separate level.
• The Missing Levels per column. This is either 0 (no missing values) or 1 (one or more missing values).
• The Nonmissing Levels, i.e. the number of distinct values. A missing value isn’t considered as a separate level.

By default, the FREQ procedure only shows the result on your screen. However, we need a dataset of the results to remove the empty columns later on. So, we use the ODS to create an output dataset.

/* CREATE TABLE WITH NNONMISSLEVELS */
ods select nlevels;
proc freq data=work.my_data nlevels;
ods output nlevels=work.nlevels_my_data;
run;

In the table below, you can observe that column2 and column4 have zero Nonmissing Levels. Hence, these columns are empty and need to be removed.

How to Remove Empty Columns in SAS

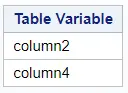
Now that we have identified the empty columns, we can remove them. We use the dataset created in the previous section and the select into clause to create a macro variable with the names of the empty columns. See the SAS code below.

/* SAVE COLUMNS NAME OF EMPTY COLUMNS */
proc sql;
	select TableVar into :empty_columns separated by ","
	from work.nlevels_my_data
	where nnonmisslevels = 0;
quit;

Finally, we use the SQL procedure to remove the empty columns. We use the ALTER TABLE statement to modify the original dataset and the DROP statement to remove the empty columns. Since the drop statement is followed by a macro variable with the empty column names, this code is generic and can be used each time to identify and remove empty columns in SAS.

/* REMOVE MISSING COLUMNS */
proc sql;
	alter table work.my_data
	drop &empty_columns.;
quit;

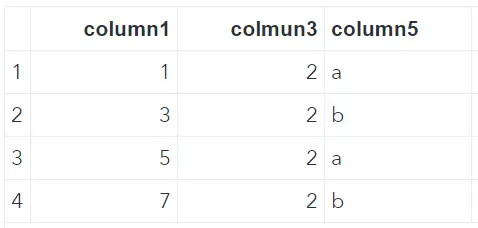
After the alter table statement our example data looks like this. Exactly how we want it.